Stable diffusion
Stable diffusion explained
Generative Modeling by Estimating Gradients of the Data Distribution.
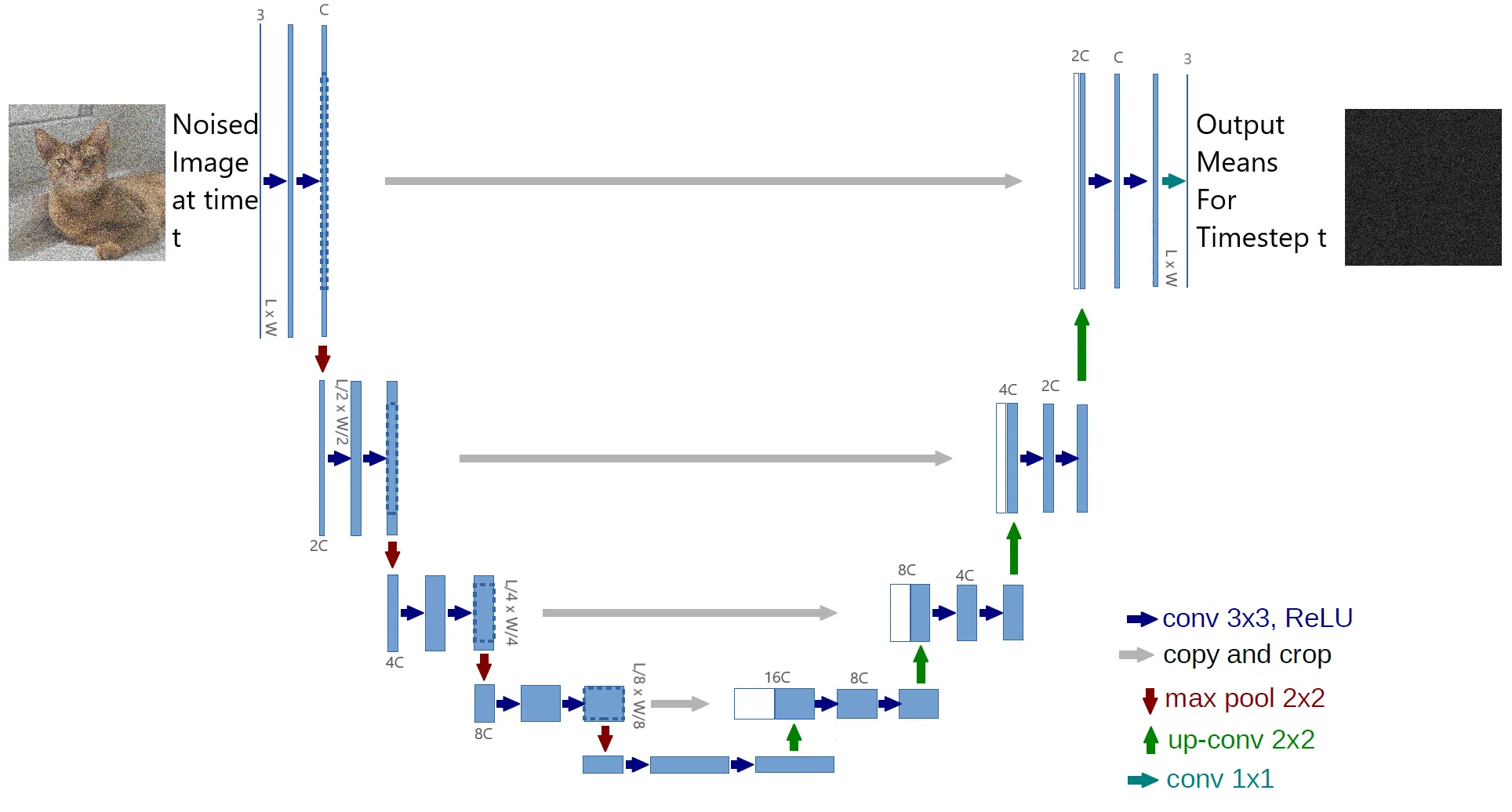

Diffusion process system information analysis:

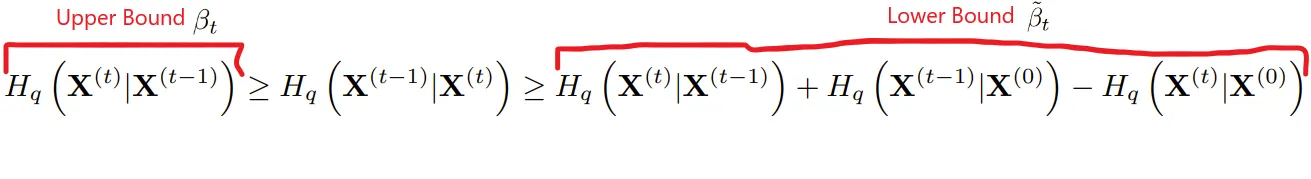
Since \(X^{(t)}\) is from adding Gaussian noise to \(X^{(t-1)}\) and Gaussian distribution alteration maximizes the entropy increase, therefore \(H_q(X^{(t)}|X^{(t-1)}) >= H_q(X^{(t-1)}|X^{(t)})\). In order words, \(H_q(X^{(t-1)}|X^{(t)})\) has less randamness than the corresponding Gaussian noise.
“A lower bound on the entropy difference can be established by observing that additional steps in a Markov chain do not increase the information available about the initial state in the chain, and thus do not decrease the conditional entropy of the initial state.” (page 12 original paper)
For the lower bound, any information gain against the initial state, i.e. \(H_q(X^{(t)}|X^{(0)}) - H_q(X^{(t-1)}|X^{(0)})\), could possiblily be introduced during the last process from \(t-1\) to \(t\), so when we remove that gained information entirely, we get the lower bound of the amount of the information.
Based on which, the improved DDPM paper decides to learn the variances to help improve the model’s log-likelihood by representing the variances as an log domain interpolation between the upper and lower bounds.
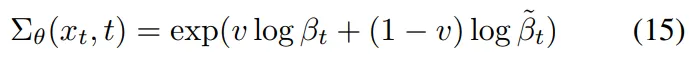
The difference between distributions is a great way to model the variance because the variance at any step should model how much the distribution changes between timesteps.
These bounds are very useful to have the model estimate the variance at any timestep in the diffusion process. The improved DDPM paper notes that βₜ and βₜ~ represent two extremes on the variance (when the equal sign holds). One when the original image, x₀, is pure Gaussian, and the other when the original image, x₀, is a single value. Any input image x₀ will fall either between a pure Gaussian or a single-valued image, making it intuitive to interpolate between these two extremes.
Stable diffusion practice
The Annotated Diffusion Model .
Github of pytorch denoising diffusion by lucidrains.
OpenAI guided-diffusion.
References
- Concept of variational lower bound (also called ELBO) in variational auto-encoder (VAE) introduced by Kingma et al., 2013.
- U-Net introduced by Ronneberger et al., 2015.
- A Recipe for Training Neural Networks
Enjoy Reading This Article?
Here are some more articles you might like to read next: